Фактор сжимаемости газа

Как известно, уравнение состояния устанавливает функциональную связь между давлением p, объемом V, температурой T и числом молей n газа в состоянии равновесия. Эта связь может выражаться не только в форме уравнения, но также графически или в виде таблиц, которые часто используются, особенно для практических целей. Самым простым и известным уравнением состояния является уравнение состояния идеального газа:

pV = nRT (1.1)

где R – универсальная газовая постоянная.

Реальные газы описываются уравнением состояния идеального газа только приближенно, и отклонения от идеального поведения становятся заметными при высоких давлениях и низких температурах, особенно когда газ близок к конденсации.

Так, для газов с низкой температурой сжижения (He, H₂, Ne и даже N₂, O₂, Ar, CO, CH₄) при давлениях до 50 атм отклонения не превышают 5%, а при давлениях до 10 атм – 2%. Легко конденсирующиеся газы (CO₂, SO₂, Cl₂, CH₃Cl) уже при 1 атм обнаруживают отклонения до 2 – 3%.

Одной из наглядных характеристик отклонений реальных газов от идеального поведения оказывается мольный объем газа V_m = V/n. Для идеального газа он равен 22,414 л при 1 атм и 273 K. Значения V_m для некоторых реальных газов представлены в таблице 1.1.

Таблица 1.1. Мольные объемы газов при 1 атм и 273 K

Газ	V_m, л* моль -1	Газ	V_m, л* моль -1
H₂	22,43	CO₂	22,26
He	22,43	N₂O	22,25
Ne	22,42	H₂O	22,14
F₂	22,42	NH₃	22,08
N₂	22,40	Cl₂	22,02
CO	22,40	SO₂	21,89
O₂	22,39	C₄H₁₀	21,50
CH₄	22,36	O₃	21,60

Наиболее удобной мерой неидеальности является фактор сжимаемости Z = pV_m/RT, поскольку для идеального газа Z = l при любых условиях.

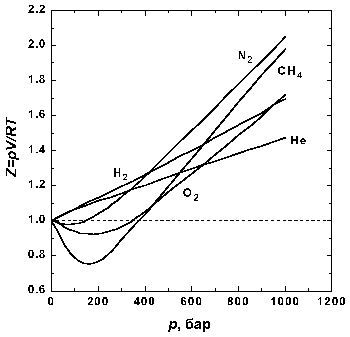
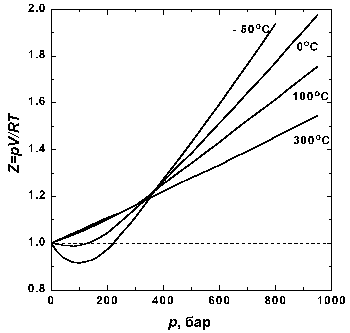
На рис. 1.2 представлены факторы сжимаемости для азота при разных температурах. По мере уменьшения температуры эффект межмолекулярного притяжения увеличивается (что проявляется в образовании минимума на кривых в области давлений около 100 бар). Минимум на кривых обнаруживается для всех газов, если температура достаточно низка. У водорода и гелия, имеющих очень низкие температуры кипения, этот минимум наблюдается только при температурах значительно ниже 0° C.

Из приведенных данных видно, что при низких давлениях реальные газы могут быть более сжимаемыми (Z 1). Очевидно, что основными причинами отклонений свойств реальных газов от свойств идеального газа оказываются взаимное притяжение молекул и наличие у них собственного объема. Наиболее ярко межмолекулярное притяжение в реальных газах проявляется в их способности к конденсации – переходу в жидкое состояние.

Рассмотрим, что происходит, когда образец газа в состоянии, отмеченном точкой А на рис. 1.3, сжимается при постоянной температуре.

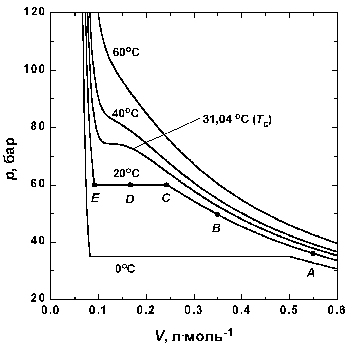
Вблизи точки А давление возрастает приблизительно по закону Бойля. Заметные отклонения от закона Бойля начинают наблюдаться, когда объем становится соизмеримым со значением, указанным точкой В.

В точке С сходство с идеальным поведением полностью теряется, так как оказывается, что дальнейшее уменьшение объема не вызывает роста давления; это показано горизонтальной линией CDE. Исследование содержания сосуда показывает, что сразу за точкой С появляется жидкость, и можно наблюдать две фазы, разделенные резко обозначенной границей – поверхностью раздела. Поскольку при уменьшении объема газ конденсируется, он не оказывает сопротивления дальнейшему движению поршня. Давление, соответствующее линии CDE, когда жидкость и пар находятся в равновесии, называется давлением пара жидкости при температуре опыта.

В точке Е весь образец представляет собой жидкость, и дальнейшее уменьшение объема образца требует значительного давления, поскольку жидкости по сравнению с газами очень трудно сжимаются, что проявляется в резком подъеме кривой слева от точки Е.

1.2. Критические явления

Изотерма при температуре T_c играет особую роль в теории состояния вещества. Изотерма, соответствующая температуре ниже T_c, ведет себя так, как уже описано: при определенном давлении газ конденсируется в жидкость, которую можно различать по наличию поверхности раздела. Если же сжатие осуществлять при T_c, то поверхность, разделяющая две фазы, не появляется, а точка конденсации и точка полного перехода в жидкость сливаются в одну критическую точку газа. При температуре выше T_c газ невозможно обратить в жидкость никаким сжатием. Температура, давление и мольный объем в критической точке называются критической температурой T_c, критическим давлением p_c и критическим мольным объемом V_c вещества. Собирательно параметры p_c, V_c, и T_c называются критическими константами данного газа (таблица 1.2).

Таблица 1.2. Критические константы и температуры Бойля

Газ	T_c, K	P_c, бар	V_c, мл* моль -1	Z_c	T_B, K	T_B/T_c
He	5,21	2,27	57,76	0,305	22,64	4,35
Ne	44,44	26,9	41,74	0,307	122,1	2,75
Ar	150,72	48,0	75,25	0,292	411,5	2,73
Kr	209,4	54,3	92,24	0,291	575,0	2,75
Xe	289,75	58,0	118,8	0,290	768,0	2,65
H₂	33,3	13,0	65,0	0,306	110,0	3,30
N₂	126,1	34,0	89,5	0,292	327,2	2,60
O₂	154,4	50,5	73,4	0,292	405,9	2,63
CO₂	304,2	73,8	94,0	0,274	714,8	2,35
CH₄	190,7	46,0	99,0	0,287	510,0	2,67
C₂H₄	282,4	50,4	129,0	0,277	624	2,21

При T T_c образец представляет собой фазу, полностью занимающую объем содержащего ее сосуда, т. е. по определению является газом. Однако плотность этой фазы может быть значительно большей, чем это типично для газов, поэтому обычно предпочитают название «сверхкритический флюид» (supercritical fluid).

В критической точке изотермический коэффициент сжимаемости 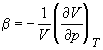равен бесконечности, поскольку 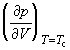= 0. Поэтому вблизи критической точки сжимаемость вещества так велика, что ускорение силы тяжести приводит к значительным различиям плотности в верхней и нижней частях сосуда, достигающим 10% в столбике вещества высотой всего несколько сантиметров. Это затрудняет определение плотностей (удельных объемов) и, соответственно, изотерм p – V вблизи критической точки. В то же время критическую температуру можно определить весьма точно как такую температуру, при которой поверхность, разделяющая газообразную и жидкую фазы, исчезает при нагревании и вновь появляется при охлаждении. Зная критическую температуру, можно определить критическую плотность (и, соответственно, критический мольный объем), пользуясь эмпирическим правилом прямолинейного диаметра (правило Кальете-Матиаса), согласно которому средняя плотность жидкости и насыщенного пара является линейной функцией температуры:

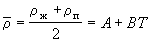, (1.2)

где A и B – постоянные для данного вещества величины. Экстраполируя прямую средней плотности 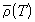до критической температуры, можно определить критическую плотность (см. задачу 1.7).

Высокая сжимаемость вещества вблизи критической точки приводит к росту спонтанных флуктуаций плотности, которые сопровождаются аномальным рассеянием света. Это явление называется критической опалесценцией.

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Теоретическая часть

Расчет фактора сжимаемости

Фактор сжимаемости учитывает отклонения реального газа от уравнения состояния идеального газа (уравнение Менделеева — Клапейрона) и представляет собой функцию температуры и давления, или функцию приведенных температуры и давления, а для смесей — функцию псевдоприведенной температуры и давления. Для идеальных газов, в которых отсутствует взаимодействие между молекулами, справедлив закон Клайперона, который обобщает законы Бойля-Мариотта и Гей-Люссака:

(P · V) / T = (P0 · V0) / T0 = R, (2.1)

где R ? универсальная газовая постоянная.

Для реальных газов произведение объема на давление (P · V) при постоянной температуре не является постоянной величиной. С ростом давления, это произведение вначале уменьшается до определенного предела, а затем с увеличением давления увеличивается. При практических расчетах для оценки степени указанных отклонений в уравнение Клайперона вводится поправочный коэффициент Z. Уравнение Клайперона — Менделеева с учетом коэффициента сжимаемости имеет вид

PV = ZNRT, (2.2)

где Р — абсолютное давление,

V — объем, занимаемый газом (газоконденсатной смесью) при определенных давлении и температуре,

R — универсальная газовая постоянная,

N — число молей газа.

Для расчета коэффициента сжимаемости, интересующего нас вещества, используем уравнение (по модификации Ли-Кеслера):

Где Z (0) — коэффициент простого вещества и рассчитывается по формуле:

А Z (R) — коэффициент эталонного вещества:

Расчет вязкостей компонентов при низких давлениях

Метод Голубева, основанный на преобразовании Трауца:

Размерность искомой величины м — мкПа•с.

В этом выражении м_kr * определяется по выражению:

где M — молекулярная масса; P_kr — критическое давление, МПа; T_kr — критическая температура, К.

Расчет SO₂ (для T = 317.16 К (40 o C))

Рассчитанная величина — 138,241 мкП

Литературные данные — 135 мкП

Соотношение Тодоса для неполярных газов:

Для полярных газов с водородной связью (T_r o C))

Рассчитанная величина — 135,196 мкП

Литературные данные — 135 мкП

Райхенберг предложил другое соотношение, основанное на использовании принципа соответственных состояний:

Также, для органических соединений Райхенберг рекомендует использовать

Расчет ацетилена (для T = 374.16 К (101 o C))

Рассчитанная величина — 126,927 мкП

Литературные данные — 126 мкП

Существующие методики расчета вязкости газа, при давлениях близких к атмосферным, в большинстве случаев, базируются или на теории Чэпмена-Энскога, или на принципе соответственных состояний.

Уравнение Чэпмена-Энскога для вязкости имеет вид:

где M — молекулярная масса; T — температура, K; у — параметр потенциала Леннарда-Джонса, Е; Щ_х — интеграл столкновений.

Чтобы использовать его для расчета вязкостей, необходимо найти параметр потенциала Леннарда-Джонса и интеграл столкновений.

Параметр потенциала Леннарда — Джонса определяется из уравнения (для неполярных газов):

где щ — фактор ацентричности; P_kr — критическое давление, МПа; T_kr — критическая температура, K;

Интеграл столкновений для неполярных газов определяется по выражению Нойфельда:

Для нахождения Щ_х сначала вычисляют величину:

где соотношение е / k определяется по выражению Ти, Готоха и Стьюарта:

где щ — фактор ацентричности; е — параметр потенциала Леннарда-Джонса, эрг; k = 1,3805•10-16, эрг/K — постоянная Больцмана.

Фактор сжимаемости газа

Назначение и формула расчета коэффициента сжимаемости грунта

Грунт под влиянием внешних сил и собственного веса может деформироваться, уменьшится в объеме. Происходит его уплотнение. Это свойство получило название «сжимаемость». Показатель учитывается при строительстве. Для определения пригодности участка к застройке проводят бурения пробных скважин, исследования отобранных пород в лабораторных условиях.

Показатели сжимаемости грунта

Характеристики почвы на деформацию определяются двумя методами:

В жестких, не поддающихся растяжению, компрессионных устройствах. В них полностью исключается боковое расширение.
В условиях возможного бокового расширения.

К показателям деформирования породы относят:

коэффициент сжимаемости;
относительной сжимаемости;
модуль деформации;
структурную прочность.

Коэффициент сжимаемости

Первый показатель, изменение рыхлости породы под давлением, крайне важен. Он определяет зависимость конечного деформирования почвенной смеси от давления и дает возможность установить формат осадка основания строения.

Коэффициент относительной сжимаемости

Это параметр деформации относительно единицы давления. При определении этого показателя учитывают: усадку образца под разным нажимом от 0 до p1, начальную высоту исследуемого материала в мм и уровень пористости.

Коэффициент сжимаемости, m0, связан с модулем поперечной деформации E0 (упругости). Степень поперечного расширения для разных песков, супесей, суглинков, глин, отличается.

Выделяют три категории грунта:

сильно сжимаемый – m0 >0,5 (МПа)-1
средне сжимаемый – 0,1>m0 >0,5 (МПа)-1
мало сжимаемый – m0 Модуль упругости

Эта величина переменная. Она меняется: от степени сдавливания, времени воздействия, плотности породы, площади штампа. Чтобы спрогнозировать поведение почвенного слоя в условиях сдавливания, необходимо знать эти показатели.

Структурная прочность

Степень уплотнения зависит от структуры почвы, рыхлости, наличия кристаллизационных связей. Структурная прочность – это параметр напряженности, при котором происходит разрушение связей. Небольшие нагрузки вызывают легкую деформацию, при этом коэффициент пористости практически остается неизменным. При усилении нагрузок и достижении структурной прочности происходит перекомпоновка частиц, уплотнение и уменьшение пористости.

Формула расчета коэффициента сжимаемости

По итогам тестов составляется график компрессионной кривой. Параметр сжимаемости рассчитывается по формуле:

Чтобы его вычислить, необходимо определить соответствующий интервал давлений.

Р1 – напряжение от собственного веса грунта
Р – дополнительное давление от внешней нагрузки
Р2 – полное напряжение (Р2 = Р1 + Р)
е1, е2 – коэффициенты пористости

Согласно СНиП, полученный результат:

меньше 0,005 – грунт, мало подающийся сжиманию;
равен 0,005 – средне сжимаемый;
свыше 0,05 – сильно деформируемый.

Приборы для определения сжимаемости

Исследования и определение вида грунта проводятся с помощью компрессионных приборов, одометров. Устройство состоит из: корпуса, компрессионного кольца, штампов и индикаторов. При каждой степени нагрузки считывают показатели.

По результатам бокового давления, объему выделенной жидкости в водонасыщенных почвах определяют: коэффициент уплотнения, модуль деформации, структурную прочность.

Второй прибор, определяющий степень деформации, – стабилометр. Устройство представляет собой цилиндрическую камеру. Различают стабилометры с вертикальной или горизонтальной нагрузкой.

Минус лабораторных исследований в том, что нарастание давления в приборах происходит быстрее, чем в естественной среде. Это дает несколько завышенные показатели.

Факторы, влияющие на показатель сжимаемости

На способность почвы изменяться в объеме влияют следующие факторы:

состав почвенных смесей, песчаная почва отличается малой сжимаемостью, глина с элементами натрия более сжимаема, чем с элементами кальция;
скорость нагрузки;
увеличение давления.

Последние два фактора способствуют большему уплотнению пород.

Зависимость фактора сжимаемости реальных газов от давления и температуры

Федеральноеагентство по образованию

высшего профессионального образования

«Кузбасскийгосударственный технический университет»

Кафедрапроцессов, машин и аппаратов химическихпроизводств

Методическиеуказания к лабораторной работе по курсу»Техническая термодинамика итеплотехника» для студентовспециальностей 240801 «Машины и аппаратыхимических производств», 240301 «Химическаятехнология неорганических веществ»,240401 «Химическая технология органическихвеществ», 240403 «Химическая технологияприродных энергоносителей и углеродныхматериалов», 240502 «Технологияпереработки пластических масс иэластомеров» всех форм обучения

Протокол № 7 от15.04.2008

Протокол № 7 от15.04.2008 Электронная копия

главного корпусаГУ КузГТУ

1. Цель и задачи работы

Целью настоящейлабораторной работы является исследованиевлияния давления и температуры реальногогаза на фактор сжимаемости. В качествелабораторной установки используетсявиртуальная модель поршневого компрессора,выполненная на компьютере.

Задачами исследованиямогут быть: определение зависимостифактора сжимаемости газа от давленияпри постоянной температуре или оттемпературы при постоянном давлении,сравнение различных термодинамическихпроцессов реальных газов с уравнениямипроцессов идеальных газов, определениеобласти применимости уравнений идеальныхгазов к реальным газам.

В ходе выполнениялабораторной работы студенты проводятопыты с различными газами, устанавливаютначальные параметры газа, управляютходом исследования, измеряют значенияпараметров с помощью различных приборов.

2. Теоретические положения

Газ (французскоеGazот греческого Chaos– хаос) – агрегатное состояние веществ,в котором частицы не связаны или слабосвязаны силами взаимодействия и движутсясвободно, заполняя весь предоставленныйим объем [1]. Вещества в газообразномсостоянии образуют атмосферу Земли, взначительном количестве содержатся втвердых земных породах, растворены вводе океанов, морей и рек. Солнце, звезды,облака межзвездного вещества состоятиз газов – нейтральных или ионизированных(плазмы). В отличие от твердых тел ижидкостей, объем газа значительноизменяется при изменении давления итемпературы.

Первые закономерностио поведении газов были установлены вXVII– XIXвв. В 1662 г. английский химик и физикРоберт Бойль (1627-1691), а в 1676 г. французскийфизик Эдм Мариотт (1620-1684) показали,что при постоянной температурепроизведение давления газа на его объемпостоянно (закон Бойля-Мариотта)

В 1787 г. французскийученый Жак Александр Цезар Шарль(1746-1823) установил зависимость давлениягаза от температуры при постоянномобъеме (закон Шарля)

В 1802 французскийфизик и химик Жозеф Луи Гей-Люссак (1776-1850) установил, что если давлениегаза в процессе нагрева поддерживатьпостоянным, то объем газа при нагревебудет увеличиваться пропорциональноувеличению температуры (закон Гей-Люссака)

В 1814 г. итальянскийученый Лоренцо Романо Амедео КарлоАвогадро ди Кваренья э ди Черетто (АмедеоАвогадро) (1776-1856) сформулировал закон,который гласит, что «равные объемыгазообразных веществ при одинаковомдавлении и температуре содержат однои то же число молекул, так что плотностьразличных газов служит мерой массы ихмолекул…» (закон Авогадро).

В 1834 г. французскийфизик и инженер Бенуа Поль Эмиль Клапейрон(1799-1864) объединил законы Бойля-Мариотта,Гей-Люссака и Авогадро и вывел уравнениесостояния идеального газа (уравнениеКлапейрона)

В 1874 г. русскийученый-энциклопедист Дмитрий ИвановичМенделеев (1834-1907) обобщил уравнениеКлапейрона и получил универсальноеуравнение состояния идеального газа(уравнение Менделеева-Клапейрона)

где р– абсолютное давление газа, Па; v– удельный объем газа, м3/кг;V — объем газа, м3;T– абсолютна температура газа, К; R– удельнаягазовая постоянная, Дж/(кгК);m — масса газа,кг; - молекулярная масса газа, кг/кмоль; R- универсальная газовая постоянная, R= 8314 Дж/(мольК).

Все вышеперечисленныезаконы и уравнения справедливы дляидеального газа – такого газа, в которомотсутствуют силы взаимодействия междумолекулами, а размер молекул мал посравнению с объемом газа (молекулырассматриваются как материальныеточки).

Исследованиясвойств реальных газов показали, чтоповедение реальных газов отклоняетсяот законов идеальных газов, и темзначительнее, чем выше плотность газа,т.е. при высоких давлениях и температурах.Свойства реальных газов в целом нельзяопределять по вышеперечисленнымуравнениям.

Молекулыреальных газов имеют конечные размерыи между ними существуют силы притяженияи отталкивания, действие которых влияетна все свойства реального газа. Прималых расстояниях между молекуламидействуют силы отталкивания, которыемогут достигать огромных значений, призначительных расстояниях – действуютглавным образом силы притяжения (рис.1). В связи с этим произведение давленияреального газа на его удельный объемпри изменении давления и постояннойтемпературе не остается постоянным.

Неидеальностьгаза может быть выражена факторомсжимаемости

Для идеальногогаза, подчиняющегося уравнению Клапейрона,фактор сжимаемости равен единице прилюбых значениях абсолютного давленияи температуры. Для реальных газов zможет принимать значения как меньше,так и больше единицы.

Для описаниятермодинамических свойств реальныхгазов используются различные уравнениясостояния. Простейшим из них являетсяуравнение Ван-дер-Ваальса (Ян Дидерикван дер Ваальс (1837-1923), голландский физик)

которое качественноверно описывает основные отличияреального газа от идеального (коэффициентbучитывает размер молекул, а отношение- силы взаимодействия между молекулами).

Наиболее теоретическиобоснованным является уравнениесостояния Боголюбова-Майера

где B,C,D,Eи т.д. –вириальные коэффициенты, которыевыражают через потенциальную энергиювзаимодействия молекул газа и зависяттолько от температуры.

Для расчетавириальных коэффициентов используютэкспериментальные данные по свойствамгазов и моделируют взаимодействие междумолекулами газа в виде потенциальныхфункций межмолекулярного взаимодействия,например, потенциала Леннарда-Джонса(12-6)

где - глубина потенциальной ямы (рис. 1), Дж;r– расстояние между молекулами, м; – значение r,при котором потенциал Uравен нулю.

В основу программы,разработанной для выполнения даннойлабораторной работы, положено уравнениесостояние реального газа с пятьювириальными коэффициентами, значениякоторых для различных газов определялисьпо [2].

1 Назначение и область применения

Настоящий стандарт предназначен для практического применения при косвенном определении коэффициента сжимаемости, плотности, показателя адиабаты, скорости звука, динамической вязкости и объемной удельной теплоты сгорания природного газа, его компонентов и продуктов его переработки по измеренным значениям давления, температуры, компонентного состава и плотности при стандартных условиях.

Используемые в настоящем стандарте определения и обозначения приведены в соответствующих разделах ГОСТ 30319.0.

2 Нормативные ссылки

В настоящем стандарте использованы ссылки на следующие стандарты:

ГОСТ 22667-82 Газы горючие природные. Расчетный метод определения теплоты сгорания, относительной плотности и числа Воббе

ГОСТ 30319.0-96 Газ природный. Методы расчета физических свойств. Общие положения

ГОСТ 30319.2-96 Газ природный. Методы расчета физических свойств. Определение коэффициента сжимаемости

ГОСТ 30319.3-96 Газ природный. Методы расчета физических свойств. Определение физических свойств по уравнению состояния

ГСССД 4-78 Плотность, энтальпия, энтропия и изобарная теплоемкость жидкого и газообразного азота при температурах 70-1500 К и давлениях 0,1-1000 МПа

ГСССД 8-79 Плотность, энтальпия, энтропия и изобарная теплоемкость жидкого и газообразного воздуха при температурах 70-1500 К и давлениях 0,1-100 МПа

ГСССД 17-81 Динамическая вязкость и теплопроводность гелия, неона, аргона, криптона и ксенона при атмосферном давлении в интервале температур от нормальных точек кипения до 2500 К

ГСССД 18-81 Метан жидкий и газообразный. Плотность, энтальпия, энтропия и изобарная теплоемкость при температурах 100-1000 К и давлениях 0,1-100 МПа

ГСССД 19-81 Кислород жидкий и газообразный. Плотность, энтальпия, энтропия и изобарная теплоемкость при температурах 70-1000 К и давлениях 0,1-100 МПа

ГСССД 47-83 Этилен жидкий и газообразный. Плотность, энтальпия, энтропия и изобарная теплоемкость при температурах 130-450 К и давлениях 0,1-100 МПа

ГСССД 48-83 Этан жидкий и газообразный. Плотность, энтальпия, энтропия и изобарная теплоемкость при температурах 100-500 К и давлениях 0,1-70 МПа

ГСССД 70-84 Гелий-4 жидкий и газообразный. Плотность, энтальпия, энтропия и изобарная теплоемкость при температурах 2,4-450 К и давлениях 0,05-100 МПа

ГСССД 94-86 Метан. Коэффициенты динамической вязкости и теплопроводности при температурах 91-1000 К и давлениях от соответствующих разреженному газу до 100 МПа

ГСССД 95-86 Криптон жидкий и газообразный. Плотность, энтальпия, энтропия, изобарная теплоемкость и скорость звука при температурах 120-1300 К и давлениях 0,1-100 МПа

ГСССД 96-86 Диоксид углерода жидкий и газообразный. Плотность, фактор сжимаемости, энтальпия, энтропия, изобарная теплоемкость, скорость звука и коэффициент объемного расширения при температурах 220-1300 К и давлениях 0,1-100 МПа

ГСССД 110-87 Диоксид углерода. Коэффициенты динамической вязкости и теплопроводности при температурах 220-1000 К и давлениях от соответствующих разреженному газу до 100 МПа

ГСССД 147-90 Пропан жидкий и газообразный. Плотность, энтальпия, энтропия и изобарная теплоемкость в диапазоне температур 100-700 К и давлений 0,1-100 МПа

ГСССД Р92-84 н-Алканы (С1-С8). Вторые вириальные коэффициенты и коэффициенты динамической вязкости при атмосферном давлении в диапазоне температур от нормальных точек кипения до 800 К

ГСССД Р127-85 Пропан, н-бутан и н-пентан как компоненты природного газа. Плотность, фактор сжимаемости, энтальпия, энтропия и изобарная теплоемкость, показатель адиабаты и изобарный коэффициент расширения при температурах 270-700 К и давлениях 0,1-30 МПа

3 Определение плотности

3.1 Общие положения

3.1.1 Плотность газа r вычисляют по формуле

r = т/ V . (1)

3.1.2 Плотность определяют с помощью плотномеров любого типа (пикнометрических, ареометрических, вибрационных, акустических, радиационных и др.) или косвенным методом (измерением параметров состояния среды, определения ее состава и проведения расчета).

3.1.3 В зависимости от технико-экономической целесообразности плотность контролируемых сред допускается рассчитывать: вручную, с помощью таблиц и графиков, с применением вычислительных машин и частично или полностью автоматизированных устройств.

3.2 Определение плотности чистых газов

3.2.1 Плотность газа в идеально газовом состоянии определяют по известным значениям давления р и температуры Т по формуле

r _и = 10 3 × M × p /( R × T ). (2)

За молярную массу М принимают массу одного киломоля вещества в килограммах.

Молярную массу определяют по формуле

, (3)

где А _j — масса килограмм-атома j-го элемента, входящего в состав молекулы;

п_j — количество атомов j-го элемента молекулы.

3.2.2 Плотность реального газа (далее — газ) определяют с учетом фактора сжимаемости газа z по формуле

3.2.3 Плотность газа при стандартных условиях определяется при р = р_c и Т = Т_c т.е. по соотношению

Значения R , p _c , T _c приведены в разделе 4 ГОСТ 30319.0, a M и z _c — в таблице 1 . Если измерения z_c обеспечиваются с большей точностью, чем приведенные в таблице 1 , то целесообразно применять измеренные значения.

Молярная масса M_i _, кг/моль

Фактор сжимаемости z_ci

Фактор b_i 0,5

Плотность r _ci , кг/м 3

Погрешность d _zci , %

Критическая температура T _кi , К

Критическое давление р_к _i , МПа

Температура кипения при р=р_с, Т_кп, К

Зависимость фактора сжимаемости реальных газов от давления и температуры

Методические указания к лабораторной работе по курсу «Техническая термодинамика и теплотехника» для студентов специальностей 240801 «Машины и аппараты химических производств», 240301 «Химическая технология неорганических веществ», 240401 «Химическая технология органических веществ», 240403 «Химическая технология природных энергоносителей и углеродных материалов», 240502 «Технология переработки пластических масс и эластомеров» всех форм обучения

Составители И.В. Дворовенко

Рассмотрены и утверждены

на заседании кафедры

Протокол № 7 от 15.04.2008

Рекомендованы к печати

Протокол № 7 от 15.04.2008 Электронная копия

находится в библиотеке

главного корпуса ГУ КузГТУ

1. Цель и задачи работы

Целью настоящей лабораторной работы является исследование влияния давления и температуры реального газа на фактор сжимаемости. В качестве лабораторной установки используется виртуальная модель поршневого компрессора, выполненная на компьютере.

Задачами исследования могут быть: определение зависимости фактора сжимаемости газа от давления при постоянной температуре или от температуры при постоянном давлении, сравнение различных термодинамических процессов реальных газов с уравнениями процессов идеальных газов, определение области применимости уравнений идеальных газов к реальным газам.

В ходе выполнения лабораторной работы студенты проводят опыты с различными газами, устанавливают начальные параметры газа, управляют ходом исследования, измеряют значения параметров с помощью различных приборов.

2. Теоретические положения

Газ (французское Gaz от греческого Chaos – хаос) – агрегатное состояние веществ, в котором частицы не связаны или слабо связаны силами взаимодействия и движутся свободно, заполняя весь предоставленный им объем [1]. Вещества в газообразном состоянии образуют атмосферу Земли, в значительном количестве содержатся в твердых земных породах, растворены в воде океанов, морей и рек. Солнце, звезды, облака межзвездного вещества состоят из газов – нейтральных или ионизированных (плазмы). В отличие от твердых тел и жидкостей, объем газа значительно изменяется при изменении давления и температуры.

Первые закономерности о поведении газов были установлены в XVII – XIX вв. В 1662 г. английский химик и физик Роберт Бойль (1627-1691), а в 1676 г. французский физик Эдм Мариотт (1620-1684) показали, что при постоянной температуре произведение давления газа на его объем постоянно (закон Бойля-Мариотта)

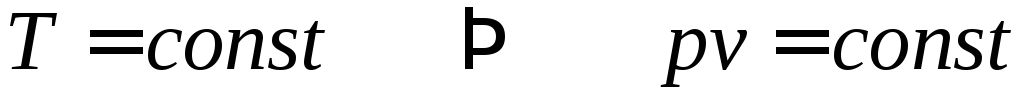В 1787 г. французский ученый Жак Александр Цезар Шарль (1746-1823) установил зависимость давления газа от температуры при постоянном объеме (закон Шарля)

В 1802 французский физик и химик Жозеф Луи Гей-Люссак (1776-1850) установил, что если давление газа в процессе нагрева поддерживать постоянным, то объем газа при нагреве будет увеличиваться пропорционально увеличению температуры (закон Гей-Люссака)

В 1814 г. итальянский ученый Лоренцо Романо Амедео Карло Авогадро ди Кваренья э ди Черетто (Амедео Авогадро) (1776-1856) сформулировал закон, который гласит, что «равные объемы газообразных веществ при одинаковом давлении и температуре содержат одно и то же число молекул, так что плотность различных газов служит мерой массы их молекул…» (закон Авогадро).

В 1834 г. французский физик и инженер Бенуа Поль Эмиль Клапейрон (1799-1864) объединил законы Бойля-Мариотта, Гей-Люссака и Авогадро и вывел уравнение состояния идеального газа (уравнение Клапейрона)

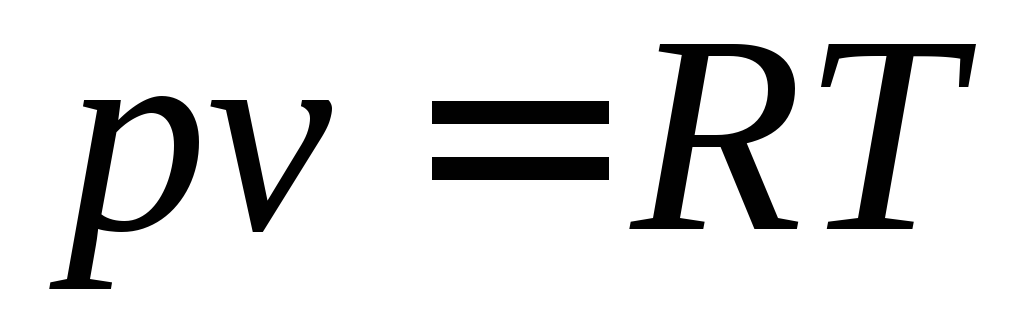В 1874 г. русский ученый-энциклопедист Дмитрий Иванович Менделеев (1834-1907) обобщил уравнение Клапейрона и получил универсальное уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

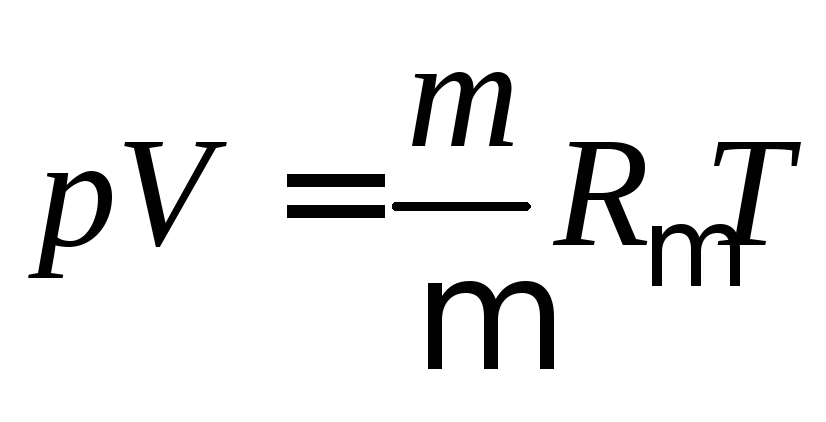где р – абсолютное давление газа, Па; v – удельный объем газа, м 3 /кг; V — объем газа, м 3 ; T – абсолютна температура газа, К; R – удельная газовая постоянная, Дж/(кгК); m — масса газа, кг;  — молекулярная масса газа, кг/кмоль; R_ — универсальная газовая постоянная, R_ = 8314 Дж/(мольК).

Все вышеперечисленные законы и уравнения справедливы для идеального газа – такого газа, в котором отсутствуют силы взаимодействия между молекулами, а размер молекул мал по сравнению с объемом газа (молекулы рассматриваются как материальные точки).

Исследования свойств реальных газов показали, что поведение реальных газов отклоняется от законов идеальных газов, и тем значительнее, чем выше плотность газа, т.е. при высоких давлениях и температурах. Свойства реальных газов в целом нельзя определять по вышеперечисленным уравнениям.

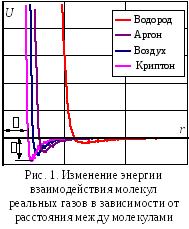Молекулы реальных газов имеют конечные размеры и между ними существуют силы притяжения и отталкивания, действие которых влияет на все свойства реального газа. При малых расстояниях между молекулами действуют силы отталкивания, которые могут достигать огромных значений, при значительных расстояниях – действуют главным образом силы притяжения (рис. 1). В связи с этим произведение давления реального газа на его удельный объем при изменении давления и постоянной температуре не остается постоянным.

Неидеальность газа может быть выражена фактором сжимаемости

Для идеального газа, подчиняющегося уравнению Клапейрона, фактор сжимаемости равен единице при любых значениях абсолютного давления и температуры. Для реальных газов z может принимать значения как меньше, так и больше единицы.

Для описания термодинамических свойств реальных газов используются различные уравнения состояния. Простейшим из них является уравнение Ван-дер-Ваальса (Ян Дидерик ван дер Ваальс (1837-1923), голландский физик)

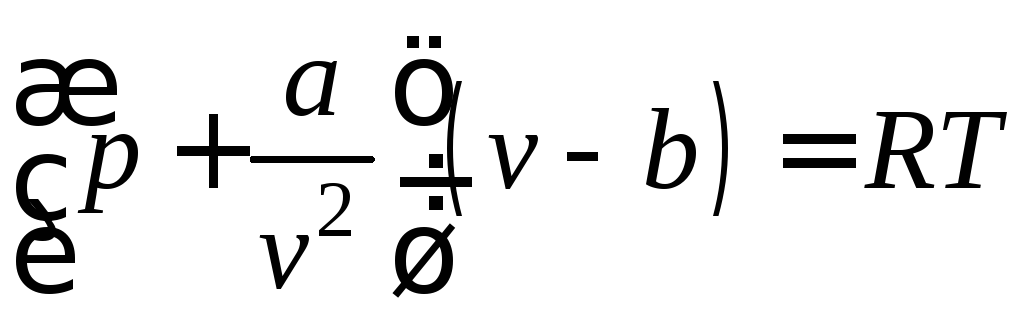которое качественно верно описывает основные отличия реального газа от идеального (коэффициент b учитывает размер молекул, а отношение 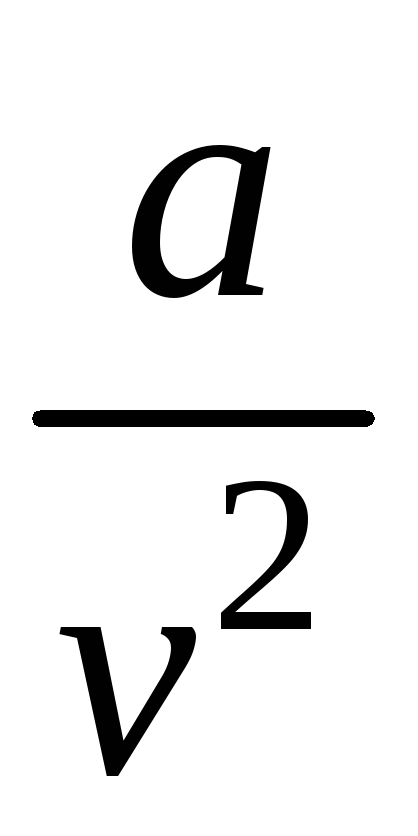— силы взаимодействия между молекулами).

Наиболее теоретически обоснованным является уравнение состояния Боголюбова-Майера

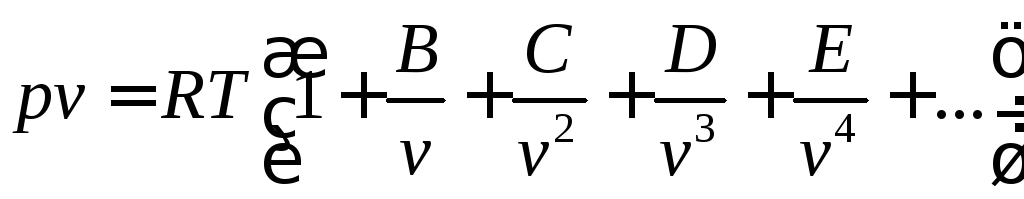где B, C, D, E и т.д. – вириальные коэффициенты, которые выражают через потенциальную энергию взаимодействия молекул газа и зависят только от температуры.

Для расчета вириальных коэффициентов используют экспериментальные данные по свойствам газов и моделируют взаимодействие между молекулами газа в виде потенциальных функций межмолекулярного взаимодействия, например, потенциала Леннарда-Джонса (12-6)

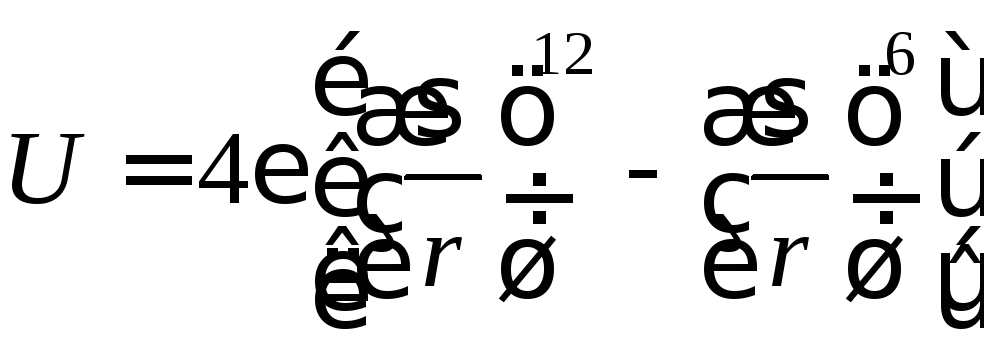где  — глубина потенциальной ямы (рис. 1), Дж; r – расстояние между молекулами, м;  – значение r, при котором потенциал U равен нулю.

В основу программы, разработанной для выполнения данной лабораторной работы, положено уравнение состояние реального газа с пятью вириальными коэффициентами, значения которых для различных газов определялись по [2].

Фактор сжимаемости газа

Фактор сжимаемости газа

Теоретическая часть

Расчет фактора сжимаемости

Расчет вязкостей компонентов при низких давлениях

Фактор сжимаемости газа