Виды давлений в гидравлике

Понятие гидростатического давления

На сайте представлено несколько статей, посвященных основам гидравлики. Этот материал адресован всем людям, которые хотят разобраться в том, как физически работают система водоснабжения и система канализации (водоотведения). Настоящая статья – первая в этом цикле.

В гидравлике есть несколько ключевых понятий. Центральное место отводится понятию гидростатического давления в точке жидкости. Оно тесно связано с понятием напора жидкости, о котором будет сказано чуть позже.

Одно из широко распространенных определений гидростатического давления звучит так: «Гидростатическое давление в точке жидкости – это нормальное сжимающее напряжение, возникающее в покоящейся жидкости под действием поверхностных и массовых сил».

Напряжение – это понятие, широко используемое в курсе сопротивления материалов. Идея в следующем. В физике, мы знаем, есть понятие силы. Сила – векторная величина, характеризующая воздействие. Векторная – это значит, что представляется в виде вектора, т.е. стрелки в трехмерном пространстве. Эта сила может быть приложена в отдельной точке (сосредоточенная сила), или к поверхности (поверхностная), или ко всему телу (говорят, массовая / объемная). Поверхностные и массовые силы являются распределенными. Только такие и могут действовать на жидкость, так как она обладает функцией текучести (легко деформируется от любого воздействия).

Сила приложена к поверхности с какой-то конкретной площадью. В каждой точке этой поверхности возникнет напряжение, равное отношению силы к площади, это и есть понятие давления в физике.

В системе СИ единица измерения силы – Ньютон [Н], площади – квадратный метр [м 2 ].

Отношение силы к площади:

1 Н / 1 м 2 = 1 Па (Паскаль).

Паскаль является основной единицей измерения давления, но далеко не единственной. Ниже представлен пересчет единиц измерения давлений из одной в другую >>>

100 000 Па = 0,1 МПа = 100 кПа ≈ 1 атм = 1 бар = 1 кгс/см 2 = 14,5 psi ≈ 750 мм.рт.ст ≡ 750 Торр ≈ 10 м.вод.ст (м)

Далее, принципиально важным моментом является так называемая шкала давлений или виды давлений. На рисунке ниже представлено, как взаимоувязаны такие понятия как абсолютное давление, абсолютный вакуум, частичный вакуум, избыточное или манометрическое давление.

Абсолютное давление – давление, отсчитываемое от нуля.

Абсолютный вакуум – ситуация, при которой на рассматриваемую точку ничего не действует, т.е. давление, равное 0 Па.

Атмосферное давление – давление, равное 1 атмосфере. Отношение веса (mg) вышележащего столба воздуха к площади его поперечного сечения. Атмосферное давление зависит от места, времени суток. Это один из параметров погоды. В прикладных инженерных дисциплинах обычно все отсчитывают именно от атмосферного давления, а не от абсолютного вакуума.

Частичный вакуум (или еще часто говорят – «величина вакуума», « разрежение» или «отрицательное избыточное давление» ). Частичный вакуум – недостаток давления до атмосферного. Максимально возможная на Земле величина вакуума как раз равняется одной атмосфере (

10 м.вод.ст.). Это означает, что у вас не получится попить воду через трубочку с расстояния 11 м при всем желании.

* на самом деле при нормальном для трубочек для напитков диаметре (

5-6 мм) эта величина будет гораздо меньше из-за гидравлических сопротивлений. Но даже через толстый шланг вы не сможете попить воду с глубины 11 м.

Если заменить вас на насос, а трубочку – на его всасывающий трубопровод, то ситуация принципиально не изменится. Поэтому воду из скважин добывают как правило именно скважинными насосами, которые опускаются непосредственно в воду, а не пытаются засасывать воду с поверхности земли.

Избыточное давление (или также еще называемое манометрическим)– превышение давления над атмосферным.

Приведем следующий пример. На данной фотографии (справа) показано измерение давления в автомобильной шине при помощи прибора манометра.

Манометр показывает именно избыточное давление. На этой фотографии видно, что избычтоное давление в данной шине приблизительно 1,9 бар, т.е. 1,9 атм, т.е. 190 000 Па. Тогда абсолютное давление в этой шине – 290 000 Па. Если мы шину проткнем, то воздух начнет под разницей давлений выходить наружу до тех пор, пока давление внутри и снаружи шины не станет одинаковым, атмосферным. Тогда избыточное давление в шине будет равно 0.

Теперь посмотрим, как определить давление в жидкости, находящейся в определенном объеме. Допустим, мы рассматриваем открытую бочку с водой.

На поверхности воды в бочке устанавливается атмосферное давление (обозначно маленькой буквой p с индексом «атм»). Соответственно, избыточное давление на поверхности равняется 0 Па. Теперь рассмотрим давление в точке X. Эта точка заглублена относительно поверхности воды на расстояние h, и за счет столба жидкости над этой точкой, давление в ней будет больше, чем на поверхности.

Давление в точке X (p_x) будет определяться, как давление на поверхности жидкости + давление, создаваемое столбом жидкости над точкой. Это называется основным уравнением гидростатики.

Для приблизительных расчетов можно принимать g = 10 м/с 2 . Плотность воды зависит от температуры, но для приблизительных расчетов может приниматься 1000 кг/м 3 .

При глубине h 2 м, абсолютное давление в точке X составит:

100 000 Па + 1000·10·2 Па = 100 000 Па +20 000 Па = 120 000 Па = 1,2 атм.

Избыточное давление – это значит за вычетом атмосферного: 120 000 – 100 000 = 20000 Па = 0,2 атм.

Таким образом, в избыточное давление в точке X определяется высотой столба жидкости над этой точкой. Форма емкости при этом никак не влияет. Если мы рассмотрим гигантский бассейн с глубиной 2 м, и трубку высотой 3 м, то давление на дне трубки будет больше, нежели на дне бассейна.

(Абсолютное давление на дне бассейна: 100000 + 1000*9,81*2 =

Высота столба жидкости определяет давление, создаваемое этим столбом жидкости.

p_изб = ρgh. Таким образом, давление можно выражать единицами длины (высоты):

Например, рассмотрим, какое давление создает столб ртути высотой 750 мм:

p = ρgh = 13600 · 10 · 0,75 = 102 000 Па ≈ 100 000 Па, что отсылает нас к единицам измерения давления, рассмотренным ранее.

Т.е. 750 мм.рт.ст. = 100 000 Па.

По тому же принципу получается, что давление в 10 метров водяного столба равняется 100 000 Па:

1000 · 10 · 10 = 100 000 Па.

Выражение давления в метрах водяного столба принципиально важно для водоснабжения, водоотведения, а также гидравлических расчетов отопления, гидротехнических расчетов и т. д.

Теперь посмотрим давление в трубопроводах. Что физически означает замеренное мастером давление в определенной точке (X) трубопровода? Манометр в данном случае показывает 2 кгс/см² (2 атм). Это избыточное давление в трубопроводе, оно эквивалентно 20 метрам водяного столба. Иными словами, если подсоединить к трубе вертикальную трубку, то вода в ней поднимется на величину избыточного давления в точке X, т.е. на высоту 20 м. Вертикальная трубка, сообщающеяся с атмосферой (т.е. открытая) называются пьезометром.

Основная задача системы водоснабжения заключается в том, чтобы в требуемой точке вода имела необходимое избыточное давление. Например, согласно нормативному документу:

[ Постановление Правительства РФ от 06.05.2011 N 354 (ред. от 13.07.2019) «О предоставлении коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов» (вместе с «Правилами предоставления коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов») ] >>> давление в точке водоразбора должно быть не менее 3 м.вод.ст (0,03 МПа)

Под точкой водоразбора можно понимать место подключения смесителя (точка 1). Эта точка находится приблизительно на расстоянии 1 м от пола, там же, где и подключение к стояку самой квартиры (точка 2) . То есть давление в этих точках примерно одинаково при закрытых кранах (вода не движется!). Давление регламентируется именно в этих точках, и, как указано выше, должно быть не меньше 3 — 6 м.вод.ст.

Однако необходимо отметить, что нормативно допустимая величина в 3 м.вод.ст – это совсем не много, так как современное сантехническое оборудование может требовать давление до 13 м.вод.ст в точке подключения для нормальной работы (подачи достаточного количества воды). Например, даже в старом СНиП по внутреннему водопроводу (СНиП 2.04.01-85*), указано, что при использовании аэратора на смесителе (сеточка, перекрывающая выходное отверстие), в точке подключения смесителя необходимо давление 5 м.вод.ст.

Основы гидравлики

Учебные вопросы:

Основные физические свойства жидкости.

В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.

Жидкости подразделяют на два вида:

• капельные
• газообразные

Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами).

К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие

Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию.К газообразным жидкостям относятся все газы.

К основным физическим свойствам жидкости относятся:

Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.

Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.

Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях

Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.

В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.

Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.

Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.

Гидростатика

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.

Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Гидростатическое давление обладает свойствами

• Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
• Свойство 2. Гидростатическое давление неизменно во всех направлениях.
• Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Основное уравнение гидростатики

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.8 ) и на ее свободную поверхность действует давление P0 . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

PdS – P0 dS – ρghdS = 0

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем:

P = P0 + ρgh = P0 + hγ

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Пьезометрический и гидростатический напоры

Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине присоединены пьезометры I и II (рис. 9).

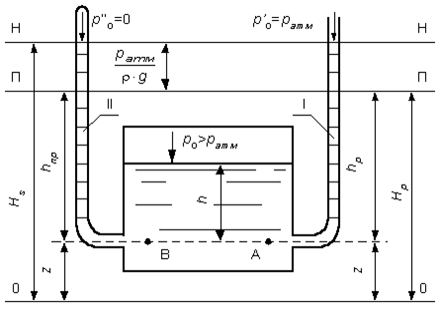
Давление на свободной поверхности в сосуде больше атмосферного. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю.

Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой. За плоскость сравнения может быть принят уровень земли, пола.

Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через – приведенная высота.

Пьезометрическая высота – мера манометрического давления в точке А. Приведенная высота – мера абсолютного давления в точке В. Разность высот , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.

Сумма геометрической высоты и пьезометрической для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:

Формулы гидравлики

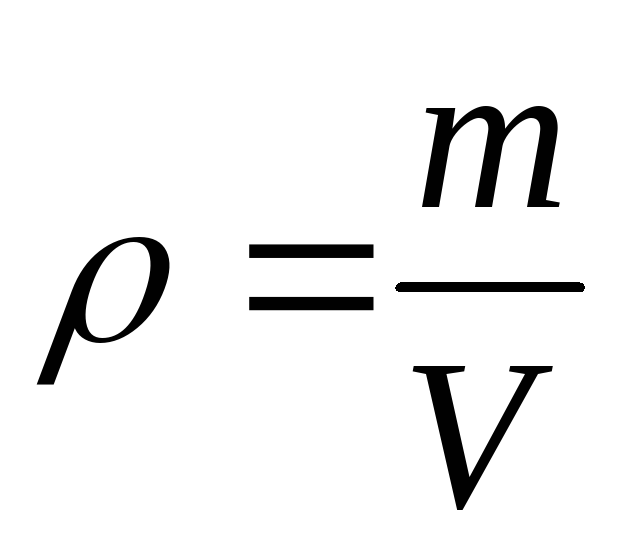(кг/м 3 ) – плотность

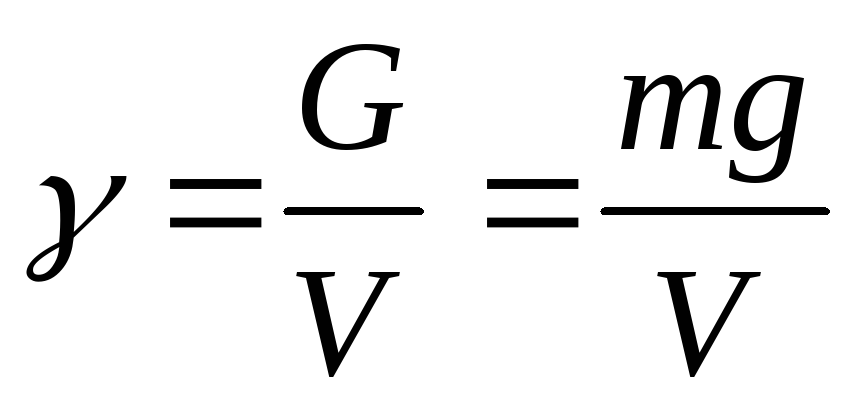(н/м 3 ) – удельный вес

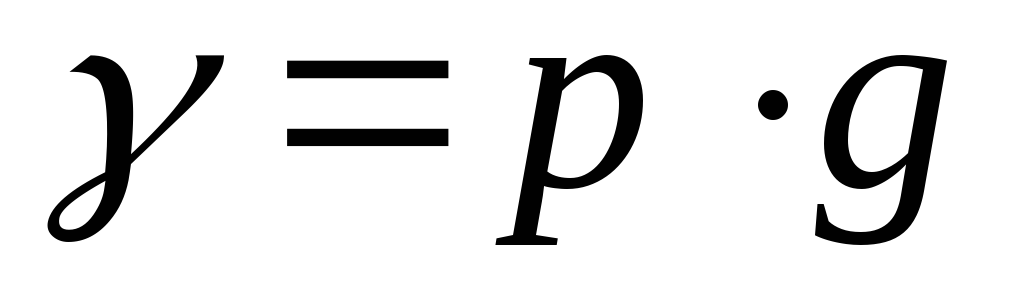
ГИДРОСТАТИКА

р — давление или сжимающие напряжение (н/м 2 = Па)

Давление всегда направлено к поверхности по внутренней нормали.

Действует одинаково по всем направлениям (не зависит от угла наклона площадки)

Основное уравнение гидростатики:

р_А = р_о + р_в; р_в = h·γ

р_А – абсолютное давление;

р_о – давление действующее на поверхность жидкости;

р_в – весовое давление, т.е. давление столба жидкости.

р_в = h·γ

h – глубина расположения точки;

γ – удельный вес жидкости.

При атмосферном давлении на поверхности:

р_А = р_а + р_изб; р_изб = h_изб·γ

р_а – атмосферное давление;

р_изб – избыточное давление.

Закон Паскаля. Давление действующее на поверхность жидкости передается во все ее точки без изменения.

Любая горизонтальная плоскость проведенная в жидкости, является плоскостью равного давления.

Можем измерять величину давления эквивалентной ему высотой столба жидкости.

р = h·γ, отсюда h = р/γ

Например давление величиной в 1 атм. р = 1 кгс/см 2 соответствует

h = 10 м вод. столба

Сила давления жидкости на плоскую поверхность

Р = р_сS = h_сγS (н)

р_с = h_сγ – давление в центре тяжести при атмосферном давлении на поверхности

р_с = h_сγ + р_М, либо р_с = h_сγ – р_ВАК

h_с – глубина расположения центра тяжести поверхности (м);

S – площадь поверхности (м 2 ).

Потенциальная энергия покоящейся жидкости величина постоянная, т.е. одинаковая для всех точек жидкости

Удельная энергия (напор) Э = Е/G = Е/mg (м)

Z + h_п = Н_ГС = Э = const

Z – геометрический напор;

h_п – пьезометрический напор;

Н_ГС –гидростатический напор или полная удельная потенциальная энергия жидкости.

ГИДРОДИНАМИКА

Q = V₁ω₁ = V₂ω₂ = const

Q – расход жидкости (м 3 /с);

V – средняя скорость потока (м/с);

Ω – площадь живого сечения потока (м 2 ).

V_i = Q / ω_i – средняя скорость потока

Уравнение Бернулли для идеальной жидкости (при действии сил давления и сил тяжести)

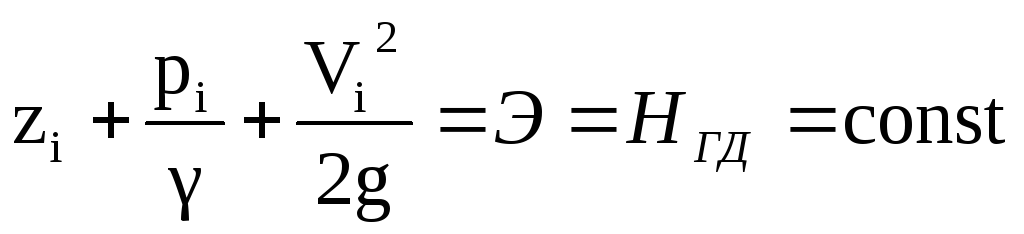
где z — геометрический напор, м;

P/γ — приведенная пьезометрическая высота (если Р — абсолютное давление) или пьезометрическая высота (если Р — избыточное давление), м;

V 2 /2g — скоростной напор, м.

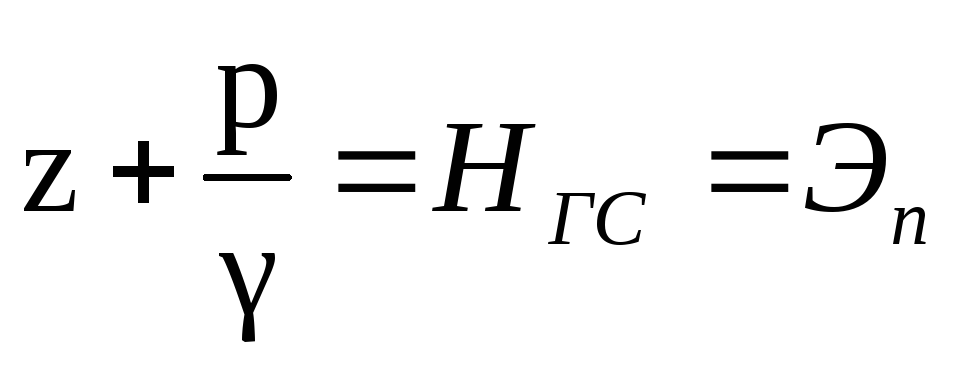— гидростатический напор,

удельная потенциальная энергия жидкости

Н_ГС = Э – гидродинамический напор или полная удельная энергия

Уравнение Бернулли для реальной жидкости (с учетом сил трения (вязкости)).

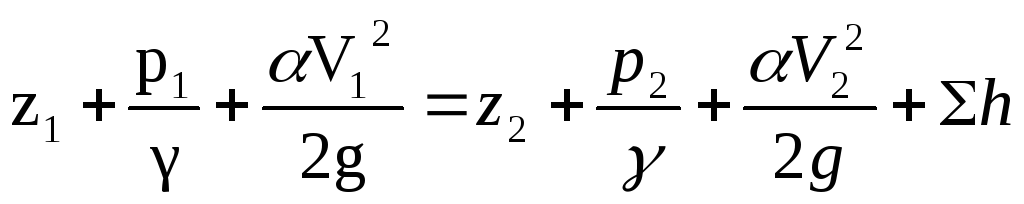
Σh = h_пот = h_ℓ + h_м – потери энергии при движении жидкости от 1 до 2 сечений (м);

α= Е_КД /Е_КУ – коэффициент кинетический энергии (коэффициент Кориолиса);

h_ℓ — потери по длине.

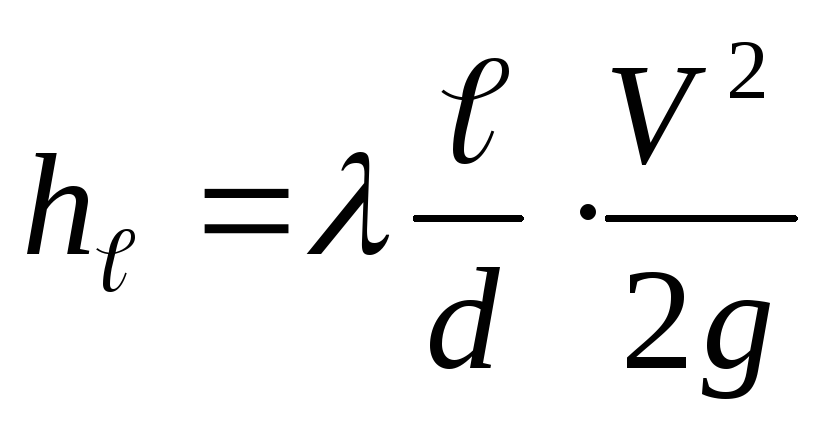(м)

λ – коэффициент гидравлического трения f(R_е·Δ);

h_м – потери на местных сопротивлениях.

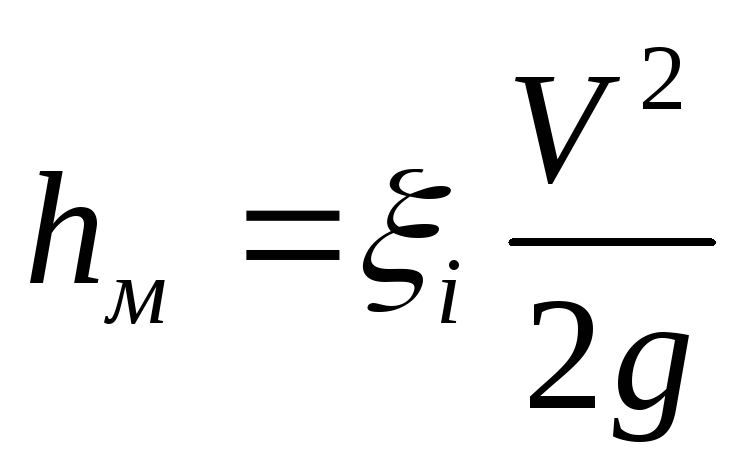(м)

РЕЖИМЫ ДВИЖЕНИЯ

Число (критерий) Рейнольдса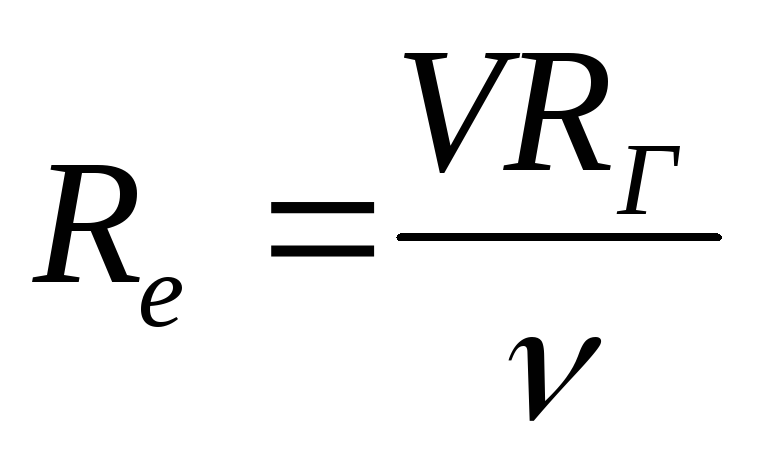

Для кругло-цилиндрических труб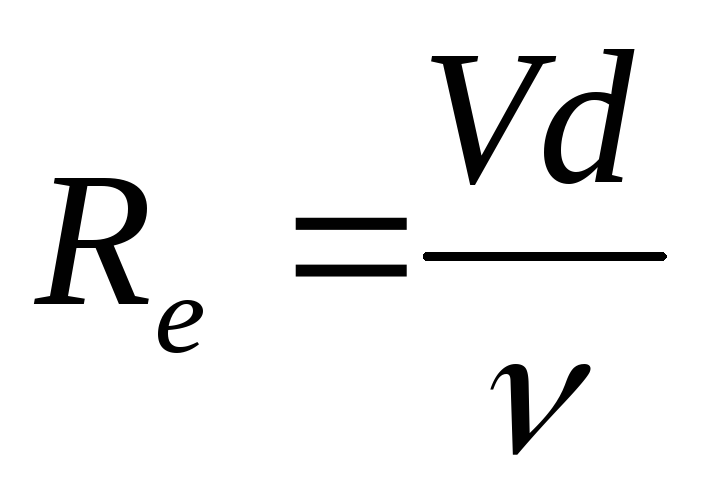

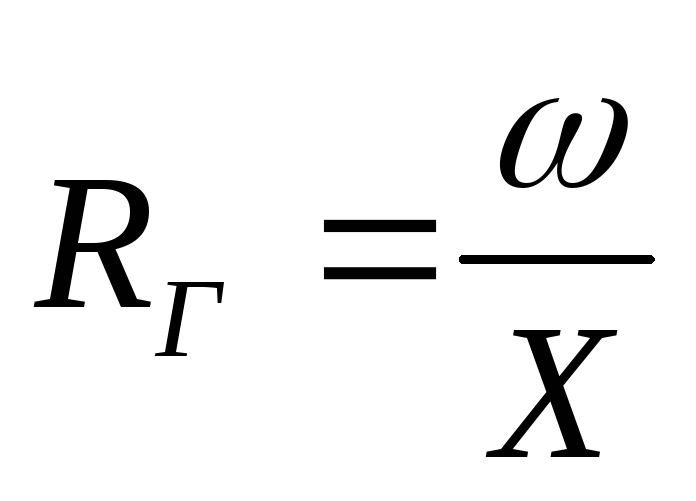(м)

R_Г – гидравлический радиус;

ω – площадь живого сечения потока (м 2 );

Х – смоченный периметр.

Ламинарный режим: Rе 1…1,4 )

Турбулентный режим : Rе > Rе_кр

Профиль скорости при турбулентном движении

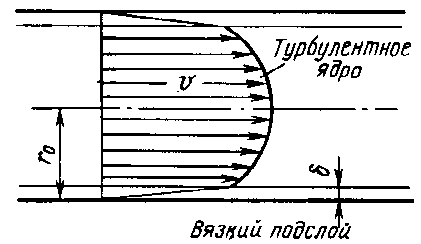
Толщина ламинарной пленки δ уменьшается с увеличением скорости V (числа Рейнольдса)

u ≈ V; α = 1…1,4

В турбулентном режиме имеется три вида трения:

Гидравлически гладкие русла

λ = f(Rе) λ = 0,3164/Rе 0,25

λ = f(Rе;Δ)

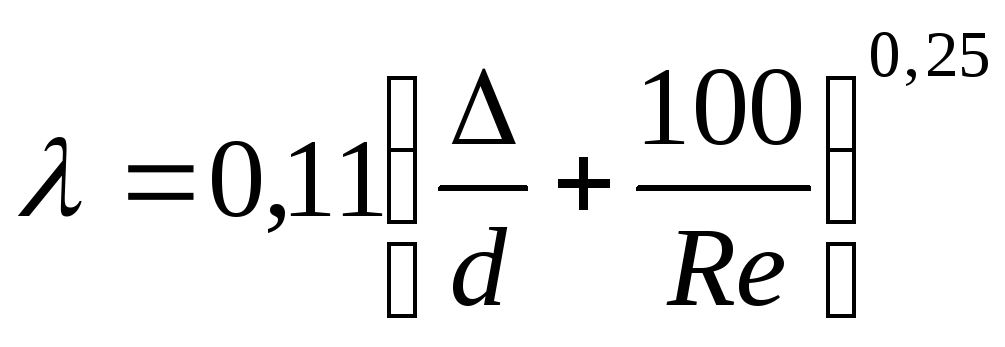
Шероховатое трение, квадратичная область турбулентного режима

λ = f (Δ); λ = 0,11(Δ /d) 0,25

h_ℓ = f (V 1,7…2 )

СКОРОСТЬ ДВИЖЕНИЯ (ИСТЕЧЕНИЯ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ

(м/с)

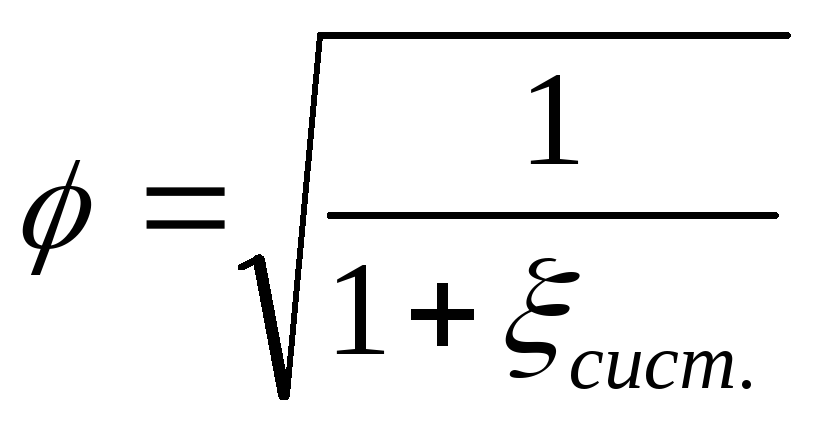— коэффициент скорости

Н_о – действующий (расчетный напор (м)

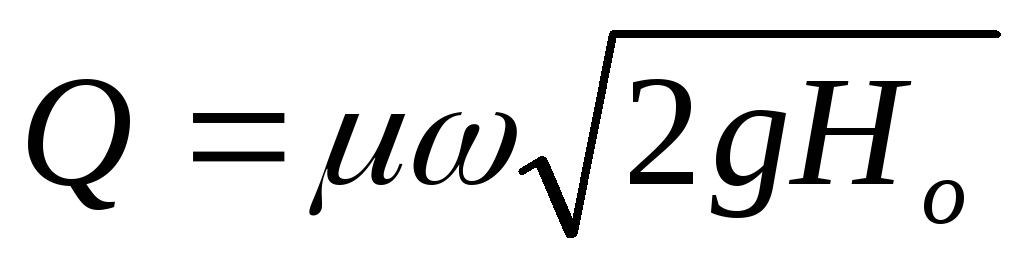(м 3 /с)

μ = φε – коэффициент расхода;

ω – площадь проходного (живого) сечения потока (м 2 );

6. Виды давления

Различают следующие виды давления: барометриче­ское, абсолютное, манометрическое и вакуумметрическое.

Барометрическое давление

Барометрическое (атмосферное) давление р_б зависит от высоты места над уровнем моря и от состояния погоды, За нормальное барометрическое давление принимают давление, равное 760 мм ртутного столба, что соот­ветствует 101325 Н/м 2 . На уровне моря барометрическое давление наблюдалось в пределах от 90 000 Н/м 2 до 110000 Н/м 2 . С высотой барометрическое давление убывает. Наоборот, в глубоких шахтах барометрическое давление значительно больше, чем на уровне моря.

Абсолютное и манометрическое давление

Давление р_а вычисленное по уравнению (6), называется абсолютным. Рассмотрим наиболее распространенный в практике случай (рис.7), когда к свободной поверхности приложено баро­метрическое давление р_б, т. е. р₀ = р₆. Для этого случая основное уравнение гидростатики перепишется так:

(15)

(16)

носит название маноме­трического, или избыточного. Таким образом, манометрическим давлением называется разность между абсолютным давлением р_а и барометрическим давлением р_б, если р_а > р_б.

Вакуумметрическое давление

Если в какой-нибудь точке жидкости абсолютное давле­ние меньше барометрического, то разность между баро­метрическим и абсолютным давлениями называется вакуумметрическим давлением. Вакуумметрическое давление обозначается р_вак. Итак, если р_а > р_б. Допустим, что требуется измерить давление на уровне 1-1. Если на этом уровне сделать отверстие и присоединить к нему стеклян­ную, трубку П, то жидкость в этой трубке поднимется под действием давления на некоторую высоту h.

По основному уравнению гидростатики (6) для точек на уровне 1-1 (если вести расчет со стороны, трубки) абсо­лютное давление

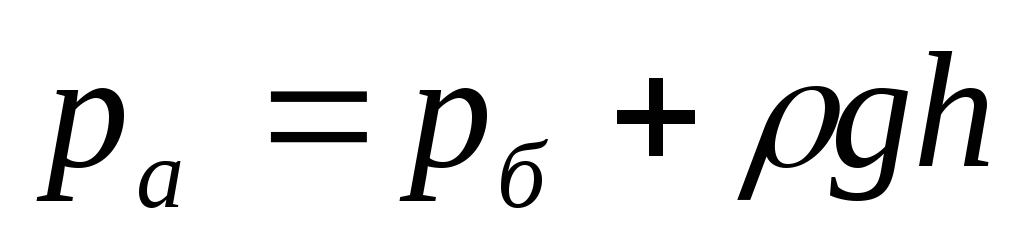
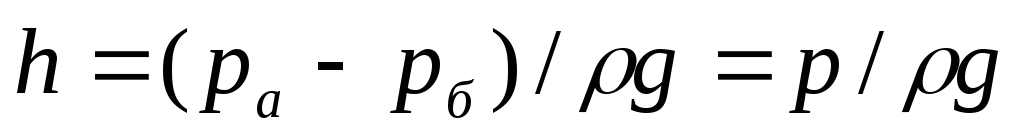(18)

Этой высотой h поднятия жидкости в трубке П можно измерять манометрическое давление. Трубка П называется пьезометром («пьезо» — давлю по гречески).

Вычислим давление в н/м 2 , соответствующее 1 м вод. ст. и 1 мм рт. ст. При высоте водяного столба h = 1 м давление р = ρgh = 9810 н/м 2 . При высоте ртутного столба h= 1 мм давление р = ρgh = 133 н/м 2 .

Для измерения вакуумметрического давления применяется вакуумметр (рис. 9).

Допустим, что требуется определить вакуумметрическое давление в сосуде S, т. е. величину р_б — р_а, где р_а — абсолютное давление в этом со­суде. Присоединяем к сосуду изогнутую трубку Т, опущенную в жидкость. Применяя основное уравнение гидростатики для точки, располо­женной в трубке Т на уровне свободной поверхности жидкости в резервуаре, получим

(19)

Таким образом, вакуумметрическому давлению будет соответствовать высота подъема h_вак жидкости в изогну­той трубке над уровнем в резервуаре.

Для измерения вакуумметрического давления применяются также приборы, действие которых подобно действию манометров. Прибор, предназначенный для измерения как манометрического, так и вакуумметрического давления, называется мановакуумметром.

Основные понятия и принципы гидравлики

Статьи о гидравлике

1. Вводная статья. Основные понятия и принципы.
2. Гидронасосы. Типы. Характеристики преимущества и недостатки различных конструкций.
3. Гидродвигатели. Типы. Характеристики преимущества и недостатки различных конструкций.
4. Гидроклапаны.
5. Коммутационная гидроаппаратура.
6. Элементы гидросистем (баки, теплообменники)
7. Устройства управления расходом. Способы регулирования расхода.
8. Устройство простейшего гидропривода.
9. Влияние внешних факторов на гидросистему.
10. Влияние загрязнений рабочей жидкости на работу гидросистемы. Фильтрация.

Основные понятия и принципы.

Введение.

Данный цикл статей рассчитан на широкий круг эксплуатантов гидравлического оборудования с различным уровнем теоретической подготовки в области гидравлики. Данный цикл статей не является полным и исчерпывающим, а несет некоторые базовые сведения о физических принципах работы гидросистем и гидравлических агрегатах. Статьи содержат в себе обзорную информацию с акцентом на вопросы, наиболее часто вызывающие затруднения у наших клиентов.

Гидравлика в наши дни прочно укоренилась в различных машинах и механизмах. Гидросистемы нашли широкое распространение в станочной технике, манипуляторах, подъемных устройствах, дорожной технике, автотранспорте, в механизмах летательных аппаратов, водного транспорта и т.д. Повсеместное применение гидравлических систем взамен систем механических приводов обусловлено прежде всего простотой преобразования вращательного движения гидронасоса в поступательное (линейное) или вращательное движение исполнительного гидродвигателя. При правильном подборе гидронасоса и исполнительного гидродвигателя можно получить практически любое усилие. Также преимуществом гидропривода является его компактность, малые размеры гидроагрегатов – следствие высокой удельной мощности. На рис.1 представлен электрический генератор мощностью 50 кВт и приводящий его гидромотор той-же мощности. Наглядно видно что гидромотор имеет заметно меньшие размеры при равной мощности.

Рассмотрим основные понятия и принципы гидравлики.

Понятие давления.

Давление это величина численно равная значению действию силы на единицу площади см. рис.2

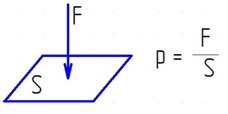
Упрощенно данную зависимость можно представить аналогично закону Ома в электротехнике:

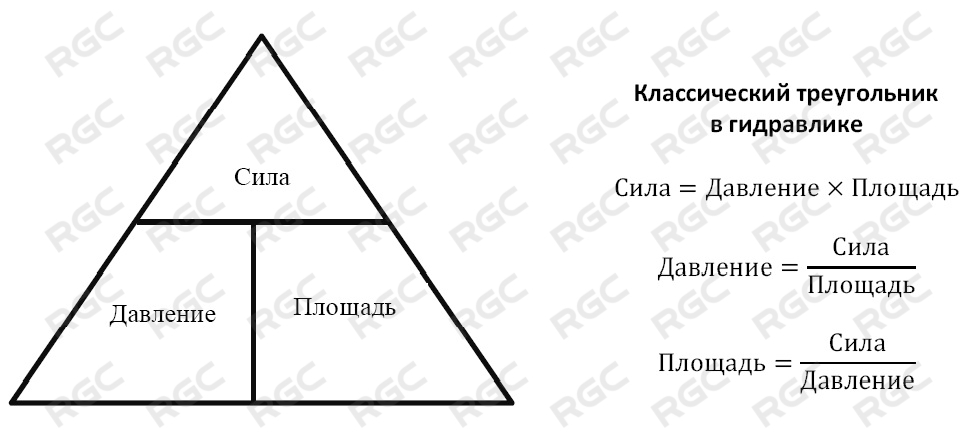
Основная единица измерения давления – Паскаль [Па]

Предположим что сила F=1 Ньютон [Н] действует на площадь 1 м2 в этом случае давление составит 1Па. Это очень маленькая величина так как усилие в 1 Н (≈0,981 кгс) распределяется на площади в 1 м2 . Атмосферное давление у поверхности земли имеет приблизительное значение 100000 Па что равняется 0,1МПа (МегаПаскаль). Кроме МПа на приборах измерения давления встречаются такие величины как кгс/см2(ат.) и bar. Соотношения единиц измерений показаны в таблице 1.

Таблица 1. Соотношения единиц измерения давления.

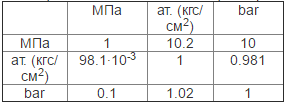
Гидростатическое давление – давление покоящегося столба жидкости.

Внутри столба жидкости под тяжестью массы жидкости, действующей на определенную площадь возникает давление, которое зависит от высоты столба жидкости (h), плотности жидкости (ρ) и ускорения свободного падения (g).

P= ρ ∙g∙h

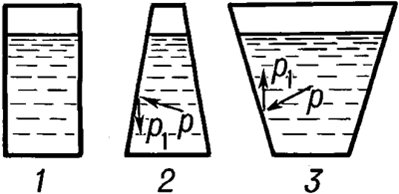
Если рассматривать различные формы сосудов, наполненных одной и той-же жидкостью то давление в определенной точке будет зависеть только от высоты столба жидкости. Р1=P2=P3 см. рис. 3.

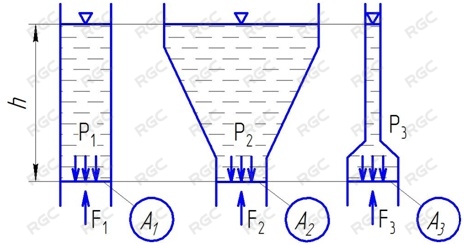
Гидростатическое давление воздействует на дно сосуда с определенной силой (F1 , F2 , F3), и если площади дна у сосудов равны A1 = A2 = A3 и плотность жидкости во всех сосудах одинакова, то силы действующие на дно сосудов равны (F1 = F2 = F3).

Закон Паскаля

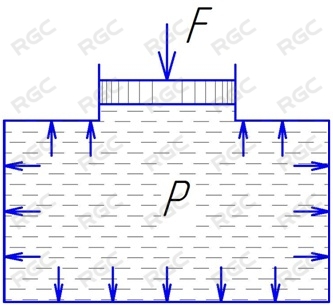
Одним из основных законов гидравлики является закон Паскаля. Он гласит что давление в замкнутом сосуде вызванное действием внешней силы равномерно распределяется во всех направлениях и одинаково в любой точке. (в данном законе не учитывается гидростатическое давление т.к. оно ничтожно мало по сравнению с значениями давлений действующими в гидросистемах). См рис.4.

Закон Паскаля лежит в основе принципа передачи усилия посредством гидравлики. Рис.5.

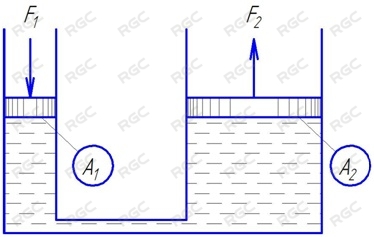
Как следует из закона Паскаля давление во всех точках рабочей жидкости одинаково, следовательно:

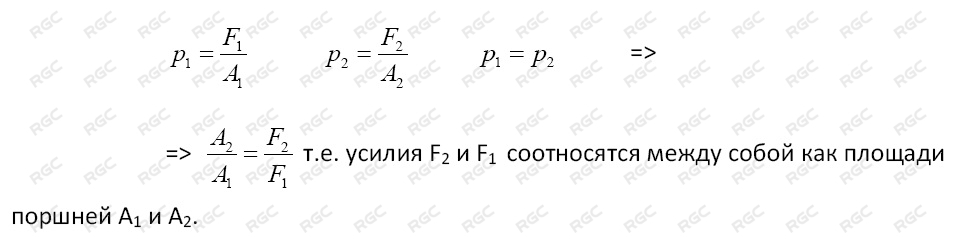
В качестве простого примера применения данного принципа может служить обычный гидравлический домкрат.

Заключение

В данной статье описаны основные принципы используемые в системах гидростатического привода. На основе этих законов построены практически все гидросистемы станочных приводов и мобильных машин. Владея всего несколькими законами гидравлики, читатель сможет выполнить силовой расчет исполнительного гидроцилиндра и оценить преимущества применения гидропривода.

Внимание! Данная статья авторская. При копировании ее с сайта обязательно указывать источник!